Research highlights

Making quantum computing more resilient

Together with our experimental collaborators at Zhejiang University, we have recently come up with a new way of making quantum particles defy the rules of statistical physics by utilising a special quantum computing device.  Generally, a bunch of quantum particles tend to spread out over time, and do not regroup. This process, known as thermalisation, is believed to be the inevitable fate of many-body quantum systems, which contain many interacting particles. Previously, we proposed that in some quantum many-body systems, the particles can regroup, acting like droplets of perfume gathering back together after being sprayed from a bottle. These systems are called quantum many-body scars (see the post below).

Our work has been published in Nature Physics and it was highlighted in press, see for example this article as well as SciTechDaily and ScienMag.

The first discovery of strongly-correlated topological states in a new material

In collaboration with Prof. Cory Dean's group at Columbia University, we have recently observed a quantum fluid known as the fractional quantum Hall states -- one of the most delicate phases of matter -- for the first time in a new two-dimensional semiconductor, tungsten diselenide monolayer (WSe2). These findings demonstrate the excellent intrinsic quality of 2D semiconductors and establish them as a unique test platform for future applications in quantum computing. The study was published in Nature Nanotechnology.

Quantum Many-Body Scars

___________________________________________________________________

How to see anyons with a scanning tunneling microscope

Ordinary particles are either fermions or bosons. Bosons like to cluster together, fermions effectively repel each other – all because of a simple ±1 sign picked up by their quantum-mechanical wave function as two particles are swapped around each other. But in a solid containing many-electrons, stranger types of particles can emerge. These new particles are collective states of many-electrons and they are called anyons because their wave function can pick up an arbitrary complex phase upon the exhange, not just ±1. As a result, statistical properties of anyons are very different from bosons or fermions, for example their charge ends up being only a fraction of the electron charge.

Where could one look for anyons? Anyons are believed to be abundant in fractional quantum Hall phases, which form in two-dimensional electron gases at cryogenic temperatures and in the presence of a strong magnetic field. Two-dimensional electron gas can be fabricated in semiconductor materials like GaAs, but more recently it can also be realised in graphene, which is an atomically thin layer of carbon atoms. Theory says that anyons form because of two essential ingredients: topology and interactions. Topology is supplied by the external magnetic field, which gives electrons the Aharonov-Bohm phase as they move around, while Coulomb interactions force the electrons to surrender their identity and “fractionalise” into anyons. There is a wealth of indirect experimental evidence supporting the existence of anyons, including the observation of their fractional charge [3] and interferometric measurements of their anyonic phase [4]. But in order to unambiguously demonstrate the existence of anyons, an experiment should measure their unique “barcode”.

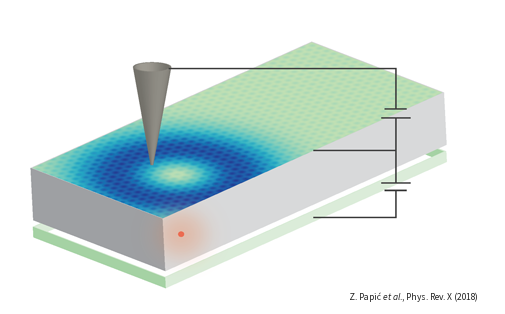In our recent paper [1], we propose to use a scanning tunneling microscope (STM) to detect the unique fingerprint of anyons in the fractional quantum Hall phases in graphene (see Figure). By ejecting an electron into the strongly-correlated fractional quantum Hall liquid in graphene, the STM is sensitive to how the electron chooses to fractionalise into several anyons. The signal of the STM, resolved in energy and momentum, is predicted to display a series of sharp levels, which correspond to bound states of the anyons. The discrete sequence of these numbers is a unique fingerprint of a fractional quantum Hall phase.

Moreover, if anyons bind to an impurity lying somewhere in the sample, the local STM spectrum is predicted to change in a specific way. The theory, proposed by Haldane in 1991 [5], which governs the counting of the STM spectrum has been known as “fractional exclusion statistics”. Thus far, it has not been possible to directly test this theory because the two-dimensional electron gases in semiconductor materials were not directly accessible. With recent advances in graphene, which hosts a two-dimensional electron gas on its surface, the STM spectroscopy of anyons becomes possible. As the paper [1] explains, this enables a new approach not only to experimentally detect anyons, but also to manipulate them. The latter would be the first step towards quantum computation with anyons – a conceptually new way to store and process information which is protected from many sources of error [6].

References
[1] Imaging Anyons with Scanning Tunneling Microscopy, Zlatko Papic, Roger S. K. Mong, Ali Yazdani, and Michael P. Zaletel, Phys. Rev. X 8, 011037 (2018); see also the accompanying synopsis in Physics.
[2] On the theory of identical particles, J. M. Leinaas and J. Myrheim, Il Nuovo Cimento B 37, 1 (1977); Quantum Mechanics of Fractional-Spin Particles, F. Wilczek, Phys. Rev. Lett. 49, 957 (1982).
[3] Direct Observation of a Fractional Charge, R. de-Picciotto, M. Reznikov, M. Heiblum, V. Umansky, G. Bunin, D. Mahalu, Nature 389, 162 (1997).
[4] Magnetic-Field-Tuned Aharonov-Bohm Oscillations and Evidence for Non-Abelian Anyons at ν=5/2, R. L. Willett, C. Nayak, K. Shtengel, L. N. Pfeiffer, and K. W. West, Phys. Rev. Lett. 111, 186401 (2013).
[5] “Fractional Statistics” in Arbitrary Dimensions: A Generalization of the Pauli Principle, F. D. M. Haldane, Phys. Rev. Lett. 67, 937 (1991).
[6] Topological quantum computation, Michael H. Freedman, Alexei Kitaev, Michael J. Larsen and Zhenghan Wang, Bull. Amer. Math. Soc. 40, 31 (2003); Introduction to Topological Quantum Computation, Jiannis K. Pachos, Cambridge University Press (2012).

__________________________________________________________________

How complex are quantum states?

Theoretical physics aims to understand the big picture of the world. This is a very complex picture because of the myriad of emergent phenomena, such as the high-temperature superconductivity or the quantum Hall effect. If we zoom in closely on one of these, all we see are ordinary electrons; but if we look at them from far away, like in the paintings by the French pointillists, a new pattern emerges, revealing fascinating properties like the current flowing without resistance. This happens because of interactions between electrons. Interactions can make particles lose their identity and behave collectively, changing the properties of the system. The problem is – the physicists’ intuition is based almost entirely on free systems, where interactions are negligible. What about more general, interacting systems like the ones above? How do we find a free system that most closely “resembles” them?

In our recent work [1], we propose a way to crack this very fundamental question. We approach quantum many-body states as biologists who befriended computer scientists: we perform the anatomy of a quantum state by decomposing it into parts, and measure its internal correlations. From this data, we evaluate the  “interaction distance” between this state and all free states. Our approach gives a new way to look at quantum states: it defines a hyperplane where all free states live, and gives us a universal “ruler” to measure the distance of any state from that plane [see Figure]. In other words, we measure the complexity of a quantum state, in the same way that the complexity of a number is specified by how many prime numbers appear in its factorisation. By factorising quantum correlations, we obtain a simple, compressed description of a quantum state, similar to modern video streaming services which provide high resolution image quality at a lower bitrate due to efficient compression.

[1] C. J. Turner, K. Meichanetzidis, Z. Papic, and J. K. Pachos, Nature Communications 8, 14926 (2017).

___________________________________________________________

Stretching and squeezing the Haldane pseudopotentials: a new language for the anisotropic fractional quantum Hall effect

In a classic paper from 1983 [1], Duncan Haldane (Nobel Prize in Physics, 2016) formulated what is now known as “the Haldane pseudopotentials” to describe the fractional quantum Hall effect. The latter phenomenon, where the Hall conductance of a two-dimensional electron gas in a magnetic field is curiously quantised in terms of rational numbers like 1/3 or 2/5, had been discovered a year earlier by Tsui, Stormer and Gossard [2]. The effect, however, remained a mystery until the early 1983 when Robert Laughlin explained it as a consequence of subtle correlations between the electrons which make them form exotic kinds of quantum fluids. (Tsui, Stormer and Laughlin shared the 1998 Nobel Prize for their discovery.) One of the crucial steps in the verification and ultimate acceptance of Laughlin’s theory came from Haldane’s pseudopotentials, which allowed to write down a rotationally-invariant wave function for the Laughlin fluid and explained why such a state could describe the real system of electrons interacting via Coulomb force.

An underlying assumption of the Haldane pseudopotentials has been that the electron system is rotationally invariant – it looks the same in x and y directions. However, it is known that experimental semiconductor systems, which realise the quantum Hall effect, are not rotationally invariant: for example, semiconductors often have different effective masses along x- and y-directions. A natural question then arises: can Haldane pseudopotentials be defined for quantum Hall systems which are not invariant under x-y rotation?

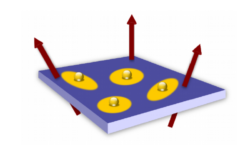
In our recent paper published in Physical Review Letters and highlighted as Editors’ Suggestion [4], we have generalised the 1983 work of Haldane by formulating the Electrons in the fractional quantum Hall states bind to magnetic fluxes, thus forming composite objects with finite area (yellow). If the magnetic field is tilted from the perpendicular direction (red arrows), the shape of particle-flux composites will fluctuate. A description of such systems requires the generalised pseudopotentials developed in Ref. [4].pseudopotentials for anisotropic fractional quantum Hall systems. This work introduces a new and universal language that allows to describe a broad class of fractional quantum Hall systems without rotational symmetry, such as experiments in tilted magnetic field, or the so-called nematic quantum Hall states which spontaneously break rotational symmetry, similar to liquid crystals. The new language also illuminates a fundamental characteristic of fractional quantum Hall fluids – their geometric degree of freedom. Such degrees of freedom determine the properties of these fluids at low energies and have recently attracted much attention because of connections with models of quantum gravity in two dimensions.

References

[1] F. D. M. Haldane, Phys. Rev. Lett. 51, 605 (1983).
[2] D. C. Tsui, H. L. Stormer, and A. C. Gossard, Phys. Rev. Lett. 48, 1559 (1982).
[3] R. B. Laughlin, Phys. Rev. Lett. 50, 1395 (1983).
[4] Bo Yang, Zi-Xiang Hu, Ching-hua Lee, and Z. Papic, Phys. Rev. Lett. 118, 146403 (2017).