String-Net Models

String-net models are 2D RG fixed-point models that support topological order and anyon excitations. The models are defined in terms of irreducible representations or `charges' of a finite group, $\mathcal{C}=\{1,$ ... $,m\}$ , that parametrise the edges of a honeycomb lattice. These charges obey the fusion rules $x\times y=\sum_{z}N_{xy}^zz$ , where $N_{xy}^z$ is the multiplicity of each fusion outcome. For each charge, $x$ , the quantum dimension $d_x$ is defined that satisfies $d_x\times d_y=\sum_{z}N_{xy}^zd_z$ . The models can be expressed with a stabilizer Hamiltonian, where $S_{v}$ and $T_{p}$ are vertex and plaquette stabilizers respectively.

$\displaystyle H = u_{1}\sum_{v}S_{v} + u_{2}\sum_{p}T_{p}$

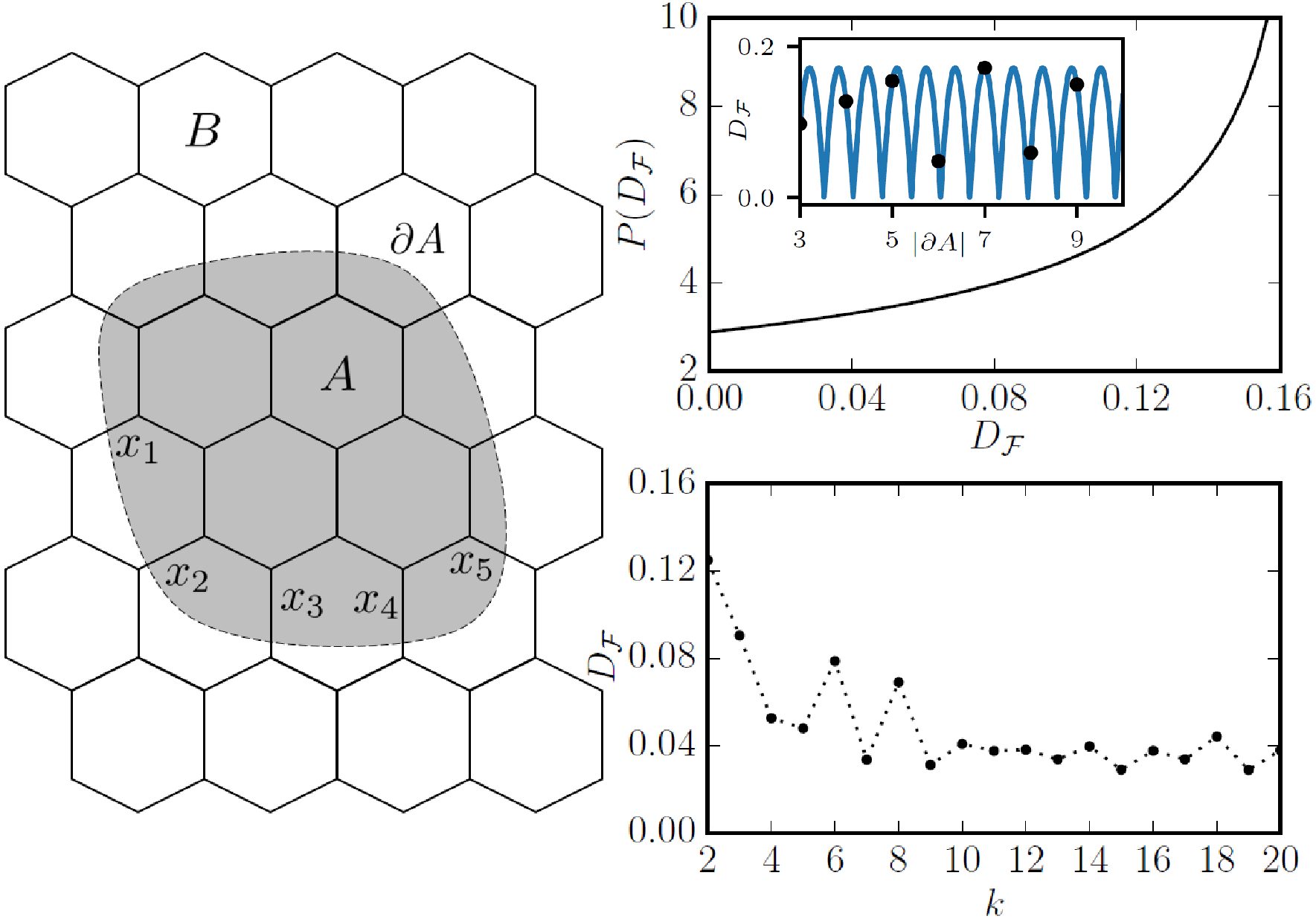
The entanglement spectrum of a bipartition of the ground state of a string-net model into $A$ and $B$ is given by

$\displaystyle \rho_a=\frac{\prod_{j\in a}d_{x_j}}{\mathcal{D}^{2(|\partial{A}|-1)}}$

where $\mathcal{D}=\sqrt{\sum_x d_x^2}$ is the total quantum dimension of the group and $x_j$ is an element of the configuration, $a$ , of charges at the boundary $\partial{A}$ , shown in the figure below (Left).

We initially consider string-nets defined with an Abelian group $\mathbb{Z}_M$ . These models have flat entanglement spectra for any bipartition with degeneracy $N=M^{|\partial{A}|-1}$ . Hence, the interaction distance $D_\mathcal{F}$ is directly determined from the upperbound for $D_{\mathcal{F}}(\bar{\rho}(N)) \leq 3 - \frac{N}{2^{n}} - \frac{2^{n+1}}{N}$ as in the case of parafermion chains, shown again in the figure below.

The cases with $M=2^y$ can be exactly described by fermionic zero modes, giving $D_{\mathcal{F}}=0$ for any partition size. Hence, the ground states of these models are Gaussian states. This is a surprising result as anyonic quasiparticles are expected to emerge in interacting systems. For $N=2$ we obtain the well known Toric Code. In the second paper we show the fermionisation of this model is given in terms of free lattice fermions coupled to a $\mathbb{Z}_2$ gauge field.

For string nets with $M\neq 2^y$ , $D_\mathcal{F}$ is always non-zero. In particular, its value depends on the size $|\partial{A}|$ of the partition boundary. We investigate its behaviour by studying the distribution $P(D_\mathcal{F})$ of $D_\mathcal{F}$ by varying the size $|\partial{A}|$ of the boundary for a certain model $\mathbb{Z}_M$ . This distribution can be shown to be given by $P(D_{\mathcal{F}})=2/(\ln 2\sqrt{1+D_{\mathcal{F}}(D_{\mathcal{F}}-6)})$ , which, surprisingly, is independent of $M$ . Hence, there exist partitions that asymptotically maximise $D_{\cal F}$ for all $M\neq 2^y$ , as shown in the first figure (Right, Top). Therefore, all $\mathbb{Z}_M$ Abelian string-nets either admit a free-fermion description for any partition or they form a class for which the manifestations of interactions are equivalent.

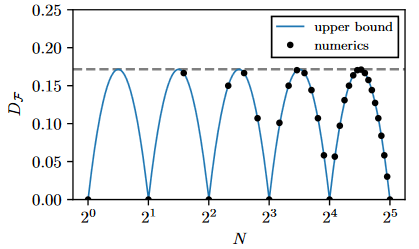
We next consider the non-Abelian string-net models. For concreteness, we take the finite group to be $SU(2)_k$ for various levels $k\geq2$ . This group gives rise to string-net models that support a large class of non-Abelian anyons, such as the Ising anyons for $k=2$ , with statistics similar to Majorana fermions, or the Fibonacci anyons for $k=3$ , that are universal for quantum computation. For simplicity we consider the interaction distance for a single site partition that has $|\partial A|=3$ . We find that $D_{\cal F}\neq 0$ for all $k\leq20$ , as shown in the first figure (Right, Bottom). Hence, it is not possible to find a free fermion description of these non-Abelian string-net models.