Definition of the Interaction Distance

The interaction distance, $D_\mathcal{F}$ , is a function of only one argument -- the interacting reduced density matrix $\rho$ :

$D_\mathcal{F} (\rho) = \underset{\sigma \in \mathcal{F}}{\mathrm{min}}D(\rho, \sigma)$

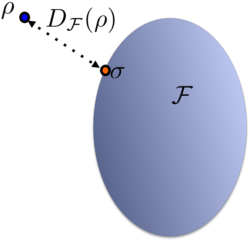
Interaction distance represents the minimum of trace distance $D(\rho, \sigma) = \frac{1}{2}\mathrm{tr}\sqrt{(\rho - \sigma)^2}$ , between $\rho$ and $\sigma$ which belongs to the manifold of free density matrices $\sigma \in \mathcal{F}$ . Note that to obtain the final value for the interaction distance we need to perform a minimisation over all possible $\sigma$ . Hence, the meaning of $D_\mathcal{F}$ is the shortest distance of $\rho$ from the manifold $\mathcal{F}$ (see Figure on the left).

$D_\mathcal{F}$ is a property of a quantum state, or more precisely its reduced density matrix $\rho$ for a specific bipartition of the system. For a spin chain of length $2N$ and equal bipartition, the manifold $\cal{F}$ is a $2^N$ dimensional space and the variational parameter $\sigma$ has the same dimension as $\rho$ , namely $2^N$ x $2^{N}$ . Fortunately the optimisation over $\sigma$ can be reduced to one with only $N$ parameters. This crucial simplification is possible due to the following theorem in linear algebra. Assume that both $\rho$ , $\sigma$ have been separately brought to diagonal form. Then, the minimum of trace distance between $\rho$ and $U \sigma U^\dagger$ , where $U$ is any unitary matrix acting on the subsystem, is achieved when $U$ is the permutation matrix. In other words, the minimum can be computed by knowing only the spectra of $\rho$ and $\sigma$ , where both spectra are arranged in the same way (for example, from largest to smallest eigenvalues). This means the optimisation need only be performed over the spectrum of $\sigma$ , which is a much simpler optimisation over a space of dimension $N$ .

The code section explains how the "esfactor" Python library, written by Christopher Turner, is used in order to perform the optimisation procedure and retrieve the value of $D_\mathcal{F}$ and the spectrum of the optimal model, $\sigma$ .