Entanglement Spectrum

The first investigations into the theory of quantum information revealed that there was a deep link between the classically understood quantity of entropy and the purely quantum mechanical phenomenon of entanglement. John von Neumann used the density matrix formalism to create a theory of quantum statistical mechanics in order to describe ensemble systems, in doing so he defined an entropy now known as the von Neumann entropy, which quantifies the subtle concept of entanglement that distinguishes quantum from classical physics. The von Neumann entropy is defined as

$\displaystyle S = -\mathrm{Tr}(\rho\ln \rho) \$

where ${\rho}$ is the density matrix that encodes a general state (usually mixed) of an ensemble system.

According to the rules of quantum mechanics, if a pure state is entangled, it means that states of its subsystems are in general not pure and thus cannot be described using a wave function. Rather, the state of a subsystem is described by an operator, which is called the reduced density matrix.

For example, if we have a lattice system which is divided as above, the reduced density matrix of subsystem A can be calculated as:

$\displaystyle \rho_A = \mathrm{Tr}_B |\psi \rangle \langle \psi| \$

To this density matrix we can now associate the von Neumann entropy:

$\displaystyle S_A = -\mathrm{Tr}_A( \rho_A \ln \rho_A) \$

When looking at a system as a composite of two or more parts, a purely quantum mechanical effect can emerge. While the entropy of the entire system is zero (if we assume the total system is in a pure state), the entropy of its subsystems may well be greater than zero. We refer to such states as entangled (as opposed to uncorrelated or "product" states, where the entropy of the subsystems is zero).

While much can be gathered about the entanglement of a quantum state from its von Neumann entropy alone, in 2008 Li and Haldane showed that the spectrum of eigenvalues of the reduced density matrix contains more complete information about the system than the von Neumann entropy, which is a single number.

For example, after a system is partitioned into subsystems ${A}$ and ${B}$ , a state of the entire system may now be expressed as a matrix with rows and columns given by the state vectors from the Hilbert space for ${A}$ and the state vectors from the Hilbert space for ${B}$ . If we have an initial Hilbert space that contains 4 spins, the basis states can be labelled as such: $|0000\rangle$ , $|1000\rangle$ , $|0110\rangle$ , etc. When we bipartition the system, each of these basis states can be split as, e.g., $|00\rangle_{A}|00\rangle_{B}$ , $|10\rangle_{A}|00\rangle_{B}$ , $|01\rangle_{A}|10\rangle_{B}$ , etc. We can then construct any state matrix with the $A$ states on one axis, and the $B$ states on the other. The ground-state matrix takes the following form, for example:

$\displaystyle V_{GS} = \bordermatrix{~ & ~ \cr |0000\rangle & -0.9 \cr |0001\rangle & 0 \cr |0010\rangle & 0.3 \cr |0011\rangle & 0.3 \cr |0100\rangle & 0 \cr |0101\rangle & 0 \cr |0110\rangle & 0 \cr |0111\rangle & 0 \cr |1000\rangle & 0 \cr |1001\rangle & 0 \cr |1010\rangle & 0 \cr |1011\rangle & 0 \cr |1100\rangle & 0.3 \cr |1101\rangle & -0.04 \cr |1110\rangle & 0 \cr |1111\rangle & -0.06} \rightarrow M_{GS} = \bordermatrix{~ & |00\rangle_{A} & |01\rangle_{A} & |10\rangle_{A} & |11\rangle_{A} \cr \langle00|_{B} & -0.9 & 0 & 0 & 0.3 \cr \langle01|_{B} & 0 & 0 & 0 & -0.04 \cr \langle10|_{B} & 0.3 & 0 & 0 & 0 \cr \langle11|_{B} & 0.1 & 0 & 0 & -0.06 \cr}$

In the context of many-body systems this is known as the Schmidt decomposition. It follows from linear algebra that the diagonal matrix, resulting from the singular value decomposition of the state matrix, contains the square-root of the eigenvalues of the reduced density matrix. Equivalently, we can construct the reduced density matrix by taking the dot product of this ground state matrix with its hermitian conjugate:

$\rho_{A} = M_{GS}^{\dagger}M_{GS}$

Either way, we call the spectrum of the eigenavalues of the reduced density matrix the entanglement spectrum of this state.

By simple inspection, the entanglement spectrum already reveals a difference between "free" and "interacting" systems. The energy levels of a system of many non-interacting free particles is constructed by filling up the available single-particle states by following Wick's theorem. Similar thing holds for the entanglement spectrum of a free system. This implies that the entanglement spectrum of free systems will necessarily be symmetric about the mean eigenenergy, as in the following case of the Ising model (which is known to be free):

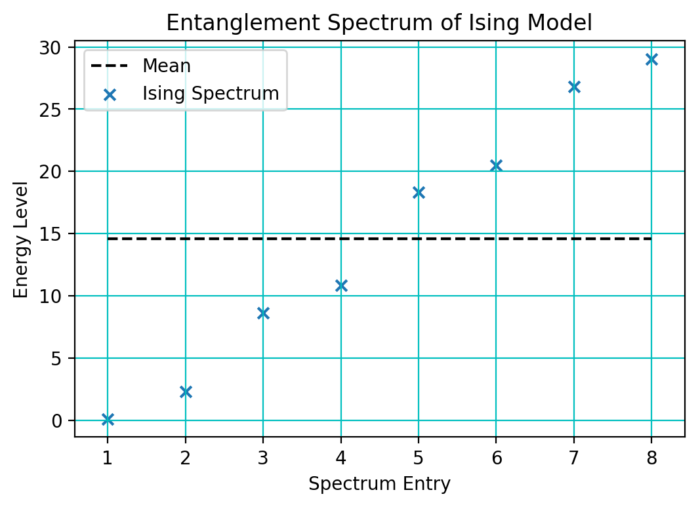
By contrast, if we add longitudinal field to the Ising model, it becomes interacting and the symmetry of the entanglement spectrum around the middle point is quickly lost:

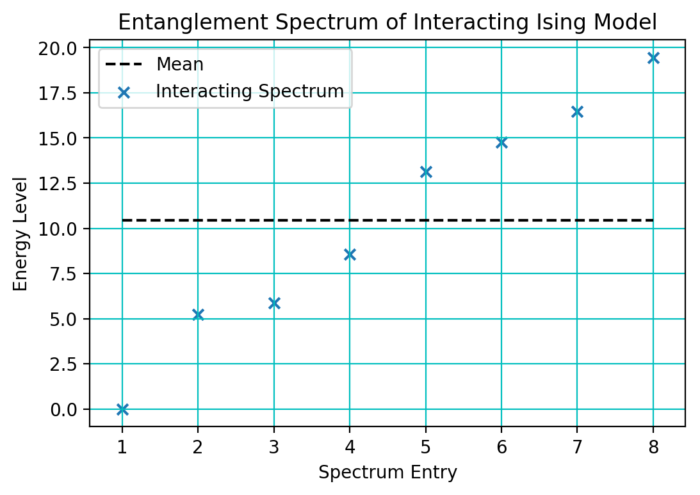
Thus, by looking at the entanglement spectrum it is possible to discern an interacting state from a free one. A more systematic way of doing this is provided by the interaction distance.