Walker-Wang Models

A generalisation of string-net models has been recently given in terms of the Walker-Wang models . These models allow non-trivial braiding of the charges giving a rich behaviour in their bulk and at their boundary.

The entanglement spectrum for topologically trivial cuts of a Walker-Wang model can be found in the same way as for string-nets given by

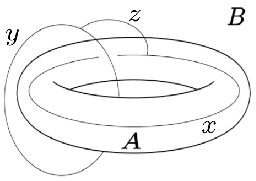
$\displaystyle \rho_a=\frac{\prod_{j\in a}d_{x_j}}{\mathcal{D}^{2(|\partial{A}|-1)}}$

Nevertheless, partitions with non-trivial boundary topology reveal novel correlation properties. To identify their effect on the interaction distance we take the region $A$ with a boundary topologically equivalent to a torus, as shown in the figure below. Among the allowed configurations in the ground state is a braiding of loops with charges $x$ and $y$ supported in $A$ and $B$ respectively, connected by a string of charge $z$ piercing $\partial A$ . Thus, the probability spectrum should now encode information about the non-trivial braiding of the charges.

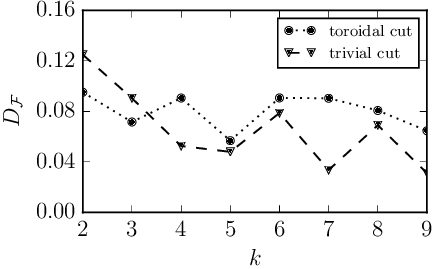
In the second figure below we show $D_{\mathcal{F}}$ for toroidal cuts of non-Abelian SU(2) $_k$ Walker-Wang models as a function of the level $k\geq2$ . Compared to the spherical cut we see that the interaction distance depends not only on the geometry of the cut but also on the topology of $\partial A$ . Its non-zero value indicates the necessity of interactions for the existence of non-Abelian topological order also in three dimensions.